作者：Bob McCarthy               翻译：易科国际

       我有一位朋友，他不是音响工程师，看完一场演出后告诉我，声音太响亮而且不够清晰。听起来很可信？当然。

       那要是另一位朋友说，听起来像是音箱阵列的连续性被打破了。这种说法还是很可信？不？

       我发现，似乎每个人都知道不连续的线阵列听起来的声音，因为这是音频界热议的话题。每次我调试系统或举行研讨会，总有人告诉我这也不能做，那也不能做，因为一旦我这么做了，就会打破线阵列的连续性：“无论如何，绝对不能打破线阵列的连续性，因为它听起来就像……”帮帮我吧，听起来像什么？

聋测&盲测
       您可以蒙住我的眼睛，领我在场地内转悠。我们可以试听粉红噪声或音乐，在场地内走动时，我将通过训练有素的耳朵告诉您声音变大了、还是变小了，混响多了还是少了，声音是明亮还是沉闷的。我还可以告诉您特定的峰值和梳状滤波区域，甚至辨识出音响系统各个要素之间的过渡，以及回声的时间与能量。并非我是什么能人异士，任何耳朵灵敏的音响工程师都能做到这点。
或者，摘除眼罩，塞住我的耳朵，将我放在远处的一所房间里，让我坐在FFT分析仪前。随着测试话筒在房间内移动，我还是可以辨认出上述特征。再次申明，我不是能人异士——任何有点眼力劲的音响工程师都能做到这点，只要他们知道如何读取分析仪并清楚声音轨迹与所听效果之间关系。

       确实，这是一种高级技能，但任何从事系统调试工作的人都应该具备。因为这些是音响系统在特定空间中客观的、可验证的和可听见的特征。两个地点之间存在6 dB的电平差，这不是理论，而是确实存在的事实，可以直接体验和测量出来。

非连续线阵列的声音
       而我无法通过上述两种方法辨别出：是否违反了线阵列理论，并且打破了线阵列的连续性。如果线阵列不连续了，我们可以听到咔哒声吗？频率响应是否显示撕裂的痕迹？这些都是很抽象的问题，但是请告诉我，什么是判断的标志？为什么大家对打破线阵列的连续性避之犹不及？

       有两种做法体现了人们“避免打破线阵列连续性”的策略。第一种是禁止在多单元组成的阵列中进行电平递变（level tapering）操作。因此，如果前区的电平比其它区域大6 dB（这是可以验证的事实，可以听出来和测量出来），有人就认为我们不应该通过电平递变解决这个问题，因为这会打破线阵列的连续性（而这是一种理论概念，无法通过声学方式或测量表现出来）。

       第二种是阵列的不同部分之间不能存在空间间隔。挑台是讨论的焦点。要覆盖高层挑台和低层挑台，我们是用一个阵列还是将阵列一分为二？答案是，选择能够实现最大一致性的方式（这是我们可以测量的）。认为阵列长度决定一切的绝对论者肯定会选择不分隔阵列，即便为了保持线阵列的完整性，一致性会受到影响也在所不惜。
现在让我们先讨论，线阵列的长度究竟有何功能。

       首先，我们要了解：当传播的波长（λ）等于辐射的锥盆尺寸时，单只扬声器的波束宽接近90度。较低频的波束宽大于90度，而较高频的波束宽小于90度。随着频率增高，波束宽越来越窄，当波长小到一定程度的时候，就会出现波瓣。

       耦合线声源的指向性也与声源的尺寸密切相关：当传播的波长λ等于线声源的长度时，覆盖为72度。如，一个两米长的阵列，170 Hz的覆盖角度是72度。170 Hz以下的频率覆盖角度越宽，而170 Hz以上的频率覆盖角度则按比例变窄。

       覆盖角度变得越来越窄时，受到频率/波长的限制，同样会出现波瓣。在这种情况下，主要由单元间隔产生的梳状干涉造成。

       1λ = 72度的标准覆盖有几个重要的附加前提。这个等式假定声源为全指向性，因此，如果声源有指向性，覆盖角度将缩小。而且，线阵列的单元数量必须足够。

       将1λ波长当成单元间360度的相位差。如果阵列由两个单元组成，声源将相距一个波长，将造成巨大的侧边波瓣（0度+360度）。同样长度的阵列如果包含三个单元，它们之间的间隔将为180度，应该引起我们的警示了。如果有五个单元，间隔将为90度，可以在混乱中产生有序的结果，抵消侧边辐射。

       除此之外，阵列的单元数量对截止频率的影响并不大。一个三米长的线阵列，不管由8个、12个还是16个单元组成，截止频率都是113 Hz。1.35米、2.7米和5.4米长的线阵列对应的截止频率分别是250 Hz、125 Hz和63 Hz。

线阵列长度的主要特征
• 标准属性只适用于全指向性声源。
• 当线阵列长度=1λ时，标称覆盖为72度；当线阵列长度=2λ时，标称覆盖为36度，以此类推。
• 指向性单元将按比例减少标称覆盖。
• 线阵列必须是连续的（足够的密度保持耦合）。

       1λ以上的频率，覆盖角度将按比例缩小。比如，线阵列长度或频率加倍时，覆盖角度变为36度。逐次加倍后，覆盖角度继续按比例缩小。1λ以下的频率，随着覆盖范围接近360度，同样的比例将不会继续保持。

       我们很容易就会夸大线阵列长度以及覆盖角度的影响。1λ频率是一个实用的参考点，但是影响不会像没有对齐的分频器那么明显。72度并不是世界上最好的覆盖角度。1λ以下的频率，其覆盖角度是逐渐、而不是突然变宽的，所以如果增加了第16只箱体，将覆盖角度降至68度的时候，不要感到太失望。

       线阵列长度只对阵列的低频产生决定性影响，如果长度不够的话，这些全指向性的单元在低频并没有指向性控制。随着频率增加以及单元的指向性增强，线阵列的长度扩展了非耦合/不明确的（近场）区域。这种扩展随着频率变化而变化，在高频处将逐渐变长。这导致在角度和距离上存在着很大的频谱变化。

       很多人都认为，线阵列长度是一个只与耦合线声源（所有箱体为0度）有关的特征。其实，耦合点声源也有长度，只不过是曲线的形式。箱体之间存在几度倾斜，对全指向性单元而言，影响微不足道。所以，同等类别的线声源和点声源之间的差别，根本无需花费时间进行分析。

       我们可以通过Goldilocks方法总结线阵列长度的行为：太大，太小和“刚刚好”（假设72度是目标的覆盖角度）。当λ大于线阵列长度时，我们拥有的控制不够；当λ小于线阵列长度时，我们拥有过多的控制；当λ等于线阵列长度时，控制刚刚好（图1）。
 

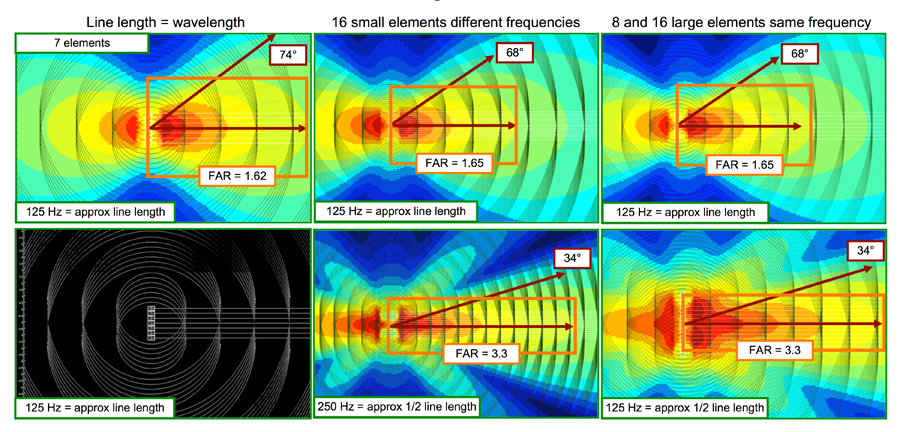
图1：线阵列长度对耦合线声源的影响；线阵列长度为2.76米（125 Hz的一个波长）。圆圈按照显示频率（见左下图）的波长设置。请注意，圆圈交集的地方具有前区波瓣，圆圈分离的地方产生抵消。当线阵列长度等于波长时（上图），不管阵列包含多少个单元，覆盖角度都大约为70度。当波长为线阵列长度的一半时，覆盖角度也减半（中下图与右下图）。

电平递变
       我们首先讨论电平递变。假设场地是一个竞技场，在垂直面上，顶部的投射距离最长，而底部的投射距离最短。那么，电平递变和打破线阵列连续性之间是数字关系吗?（即1或零？连续或不连续？）

       如果16只一模一样的箱体直线排列，并且电平相同，可以肯定这个线阵列是连续的。要是其中一只箱体电平衰减了0.1 dB，那线阵列是整个不连续了，还是只是稍微弯曲了？如果您认为整个阵列都不连续了，我要告诉您一些坏消息：您从未听过连续的线阵列，因为制造公差（Manufacturing Tolerances）远没那么好。电平之差为1 dB，情况又如何？同样，16只箱体组成的线阵列，箱体间的电平差控制在1 dB之内，没人能做到。

       让我们更进一步：将底部箱体衰减6 dB，相当于将它变为半个箱体。组合的最低频（指向性很低，波长很长，可以很好叠加）响应，衰减小于0.25 dB。在大环境中看，这个衰减并不是很吓人，对吧？

       让我们继续深入，将3只箱体衰减6 dB。现在，最低频丢失1 dB。而高频将在这三只箱体指向的区域——如前几排坐席有较大的能量衰减。这是切实好处（多达6 dB的高频控制），付出的成本最小（总体低频能量只丢失1 dB）。那现在，线阵列的连续性被打破了吗？如果它不连续了，我怎么知道呢？是整个场地都不连续，还是只在某个区域？是所有的频率都不连续吗？

       在10 kHz处，应该比较容易找到不连续的点，因为这个频率具备足够的指向性控制，如果我们的线阵列有问题，可以听见阵列两侧不连续的区域。您可以通过盲听或使用分析仪测试的方法找到它。您觉得自己能在100 Hz找到不连续的点？祝你好运了。这些大型波长活动起来可没那么灵敏。人们害怕破坏线阵列的连续性，并非担心甚高频受到影响。据我了解，他们对低频的担忧远甚于高频。

       事实应用中，电平递变是比较平缓的，步进一般为1-3 dB，使得在空间中找到过渡区域比较困难。如果我们将底部5只箱体的递变设为3-3-3-6-6 dB，整体低频将丢失1 dB，而高频的指向性将得到较大提高。在16个单元组成的阵列中，如果底部8只箱体的递变为1-1-1-1-2-2-4-4 dB，整体低频的衰减也是1 dB。这只是其中两种方法，可帮助我们根据观众席的形状，调节弯曲/不连续阵列系统的响应。

       这种递变操作可能导致一些潜在问题，但是也会带来额外的好处：除了场地前后方的高频电平更加一致之外，随着频率降低，这种一致性也将进一步提高（在较小的程度上）。我们在低频丢失的能量得到了抵消，因为波束中心向上移动，远离地面，可在场地的前后区之间实现更加均匀的分布。

增益递变的风险与好处
       在耦合的音箱阵列中，补偿电平和均衡是比较明显的风险。如果斜率和电平过渡比较平缓，可以降低风险；而陡峭的斜率和突然过渡将增加风险。

       如果单元有不同的均衡曲线，可能存在相位偏移，但是只要应用了合适的均衡处理，应该能把相位偏移降至最低。
对动态范围的影响值得详细讨论。不对称的均衡和电平递变将减少动态范围，并且可能造成动态转移（dynamic shifting），即系统的某些部分将先于其他部分到达限幅。

       天下不会掉馅饼，这就是典型的例子。这是最大一致性、稳定性和动态余量的权衡与折中。可察觉的频率不稳定性以及空间频率响应是不可以接受的结果。简而言之，动态一致性是电平和空间一致性的重要组成部分。

       电平递变对动态范围的影响（图2）可用作参考点。在这一块，节目材料与用法密切相关。如果系统一直以最大值运行（如重金属音乐节），那么前/后区的电平一致性必须让步于最大动态范围和稳定性（电平递变和非对称均衡操作需尽量避免）。

       相反，如果系统在受控状态下，以足够的动态余量运行（如音乐剧），那么非对称均衡和电平递变操作将是可行选择，使一致性达到最大。必须在场地中，基于风险与收益，经过评估后作出决定。
 

图2：八只音箱组合电平的对数/线性解码范例（不考虑相位），显示了1 dB的递变梯度，最后一栏显示了可能的最大叠加所产生的能量丢失。

       我采取的是一种折中的方法，使用最少的非对称均衡和电平调节，减少但是不完全消除房间前部分的电平提升。如果阵列的绝大部分单元都能保持较低的不对称性，风险就相对较低。阵列底部的非对称性越大，越有可能产生好的结果，并且更不容易导致上方的主体单元发挥不稳定。

       但是要知道，我的工作主要偏向应用层面，总是优先考虑一致性和保真度。而从事系统优化的工程师总是追求最大的稳定性和强劲的功率输出，相比之下，我有更多的空间接受非对称性。

       事实上，音箱的频率会重叠，重叠的范围有大有小。一个常指向性音箱组成的阵列，较高频率的重叠保持不变；而在低频，随着频率降低，重叠范围变大。因此，非对称均衡处理的有效程度与频率密切相关，高频的副作用和风险最低。

       由波束宽呈比例变化的音箱组成的阵列，频率的交叠范围也呈比例变化，也就是说，它随着波长变长而逐步、平稳变大。对整个阵列进行均衡处理时，可以将频谱切分为独立区（高频）和重叠区（低频）。可通过ABC的系统调试方法设置独立高频区的均衡和电平（将EQ分为A、B和C部分，其中两个相互参照一起调节，第三个单独调节以对整体效果进行补偿）。

       而低频部分作为一个整体进行调节，所有的均衡和电平设置都是匹配的（即对称的）。比起完全不对称的均衡处理方法，这种方法可能没办法产生那么一致的结果，但是可以消除非对称均衡处理固有的动态风险。

       我们都追求在前后区实现一致的电平，但是很多人又担心破坏线阵列的连续性。通过倾斜角度不对称调整这些系统存在限制。阵列吊挂起来后，不会再降回地面，所以我们需要知道还有多少电平差。如果前区的声音太响亮，我选择破坏线阵列的连续性，调低底部几个箱体的电平，直至或除非我们知道已经接近打破动态平衡的那个点。如果您有更好的测量和验证方法，请不吝赐教。

理论世界
       跟今天讨论主题有关的陈年趣事：30年前，当我们开始使用FFT分析仪调试音响系统时，很多工程师嘲笑我们。他们拒绝使用分析仪帮助作出决策，认为我们活在“理论世界”而他们活在“现实世界”中。

       如今，有些工程师仍然想限制我们基于分析仪而进行的操作，但很明显：我们才是活在现实世界的人，而他们活在理论世界中。很有趣，是吧？