What's actually happening with a line of loudspeakers when it's broken or tapered...
Jun. 01, 2015, by Bob McCarthy

A friend of mine who’s not an audio engineer went to a show and later told me it sounded too loud and unintelligible. Plausible? Sure.
Now try this: another friend said it sounded like the line of the loudspeakers had been broken. Still seem plausible? No?

I figure everyone knows what a broken line sounds like since it’s such a big issue for discussion in the audio community. Every time I tune a system or hold a seminar, someone tells me all the things I can’t do because I’ll break the line: “Whatever you do don’t break the line because it will sound like…” Help me out here – sound like what?

Deaf & Blind Test
I invite you to blindfold me and roll me around the venue. We can listen to pink noise or music and I’ll use my trained ears to tell you when it gets louder or softer, more reverberant or less, and brighter or duller as we move around the venue. I can tell you specific peaks and comb filter areas, and even identify transitions between elements of the sound system or the timing and strength of echoes. This is not because I’m special – any audio engineer with a trained pair of ears can do this.

Conversely, remove the blindfold, cover my ears, and put me in a remote room in front of an FFT analyzer. I can still identify these same features as a measurement microphone is moved around a room. Again, I’m not special – any audio engineer with a trained pair of eyes can do this, as long as they know how to read the analyzer and recognize the relationship of the traces to what they hear.

It’s admittedly an advanced skill, but one required of anyone tuning systems. The reason is these are objective, verifiable, audible characteristics of a sound system in a space. A 6 dB level difference between two locations is not a theory – it’s true or not true. It can be directly experienced and measured.

The Sound Of Breaking The Line
Here’s what I cannot tell you by either of the above methods: whether or not the line array theory has been violated and the line is broken. When the line breaks, do we hear a snap? Does the frequency response show tear marks? These are absurd questions but please tell me, what are the tell-tale signs? Why is there such widespread fear of breaking the line? My theory is that there’s as much or more fear of breaking the party line as the acoustical one.

There are two principal manifestations of the “don’t break the line” strategy. The first is the prohibition of level tapering within a multi-element array. So if it’s 6 dB too loud in the front area (a verifiable fact we can hear and measure) we should not solve this with level tapering because we’ll break the line (a theoretical construct we cannot characterize sonically or measure).

The second is the prohibition of spatial separation between sections of an array. Balconies are the prime movers in this discussion. Should we cover the upper and lower levels with one array or split it into two? The answer should be whichever of these can achieve the highest uniformity (something we can measure). Line length absolutists will vote to keep the array together even when this results in reduced uniformity in order to preserve the line.

Let’s take a moment to consider exactly what line length does.

We begin by noting that the beamwidth of a single loudspeaker approaches 90 degrees when the transmitted wavelength (λ) equals the radiating cone size. Lower frequencies are wider than 90 degrees and higher ones are narrower until the wavelengths are so small that lobing scatters the pattern.

A coupled line source also has a size-related directivity milestone: coverage is 72 degrees when the transmitted λ equals the line length, e.g., an array 2 meters long will be 72 degrees at 170 Hz. The coverage widens below and narrows proportionally above.

The narrowing is also frequency/wavelength-limited by lobing, in this case by the combing interaction caused by the element spacing.
Some notable conditions are attached to the 1λ = 72 degrees standard coverage. Line length equations assume omnidirectional sources, so the coverage numbers will shrink with directional elements. We also need enough quantity for the line shape to be fairly full of loudspeakers.

Think of the 1λ length as a spread of 360 degrees of phase offset over the elements. With just two elements, the sources are a full λ apart, causing a huge side lobe (0 degrees + 360 degrees). Three elements within the same length spaces them at 180-degree intervals, which should set off alarm bells. Five elements brings the spacing to 90-degree intervals, which can achieve the orderly chaos needed to cancel the side radiation.

Beyond this point the quantity has less impact on the cut-off frequency. Line lengths of 3 meters will have the same cut-off frequency (113 Hz) whether we fill it with 8, 12 or 16 elements. Line lengths of 1.35 meters, 2.7 meters, and 5.4 meters correspond to cut-off frequencies of 250 Hz, 125 Hz, and 63 Hz, respectively.

Primary features of line length:
• Standard attributes apply to omnidirectional sources.
• Nominal coverage is 72 degrees when line length = 1λ, 36 degrees when length = 2λ, and so on.
• Directional elements reduce the nominal coverage proportionally.
• Line must be effectively continuous (sufficient density to maintain coupling).

Angular reduction is proportional at frequencies above the 1λ length, i.e., we get 36 degrees when we double the length, or double the frequency. The narrowing continues with successive doublings. Simple proportionality does not hold below the 1λ frequency as the coverage approaches 360 degrees.

It’s easy to exaggerate the ramifications of line length as also often happens with coverage angle. The 1λ frequency is a convenient reference point but not something that stands out like a misaligned crossover. It’s not as if 72 degrees is the world’s greatest coverage angle. The frequencies below this marker widen gradually, not suddenly, so don’t be disappointed when adding that 16th box reduces the coverage all the way to 68 degrees.

Line length is decisive only in the very low end of these arrays, where omnidirectional elements are otherwise un-steered. As frequency rises and elements become directional, the line length extends the uncoupled/undefined (near field) area of the parallel pyramid. The extension varies with frequency, becoming steadily longer in the HF. This results in widespread spectral variance over angle and over distance.

It’s often believed that line length is a property exclusively relevant to the coupled line source (all boxes at 0 degrees). The coupled point source also has length, albeit in curved form. A few degrees of splay between boxes is negligible to omnidirectional elements, so the difference between a line and point source in the relevant range is not worth spending any time to analyze.
We can summarize the line length behavior by the Goldilocks method: too big, too small and “just right” (assuming 72 degrees is your target coverage angle). We have less than full control when λ is greater than line length, extra control when λ is less than line length, and just right control when λ equals line length (Figure 1).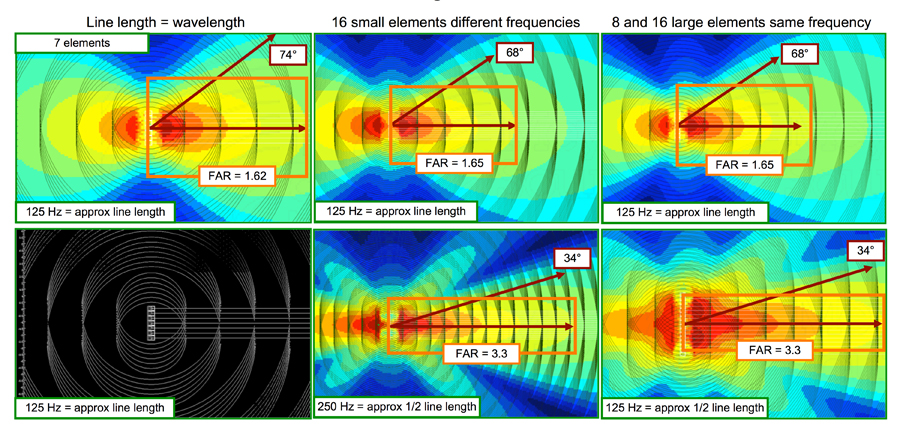  

Figure 1: The effects of line length in the coupled line source; length is a 2.76 meter (1λ at 125 Hz). The circles are sized to the wavelength of the frequency shown (lower left). Notice the front lobe follows the confluence of the circles and cancellation occurs in places where the circles diverge. The coverage angle is around 70 degrees regardless of quantity when the line length equals the wavelength (upper panels). The coverage angle is reduced by half when λ equals half the line length (lower center and right panels).

Level Tapering
Let’s start with level tapering, considering a basic arena shape in the vertical plane: longest throw to the top – shortest to the bottom. Is the relationship of level taper to line breaking a digital phenomenon? (i.e., 1 or 0? Broken or unbroken?)
It’s assured that our line is unbroken if we have a line of 16 identical boxes at the same level. If one box is turned down 0.1 dB, is the line broken or just slightly bent? If you think it’s broken already, here’s some bad news: You’ve never heard an unbroken line because manufacturing tolerances aren’t that good. How about variations of 1 dB? Again, nobody can deliver 16 boxes that are within a single dB.

Let’s step it up: Turn the bottom box down 6 dB. This makes it effectively half a box. The loss in the lowest frequency range (where directionality is so low and wavelengths so large that they sum well) that the combined response is reduced by less than 0.25 dB. This does not seem so scary in the big picture, does it?

Let’s go further and reduce 3 boxes by 6 dB. The lowest frequencies now lose 1 dB. The high frequencies, meanwhile, are substantially reduced in the area where the bottom three boxes are pointed – such as the early rows of seats. This is a tangible benefit (up to 6 dB of HF control) for a minimal cost (1 dB loss in overall LF power). Is the line broken now? If so, how can I tell? Is it broken everywhere or just at one place? Is it broken at all frequencies?

It should be easy to find the break point at 10 kHz, since there’s enough directional control to hear the isolated areas on either side of our fault line. You could find it blind-folded or measure it with an analyzer. Do you think you can identify a break point at 100 Hz? Good luck. These large wavelengths don’t turn on a dime. When people talk fretfully of breaking the line is it the VHF range they are worried about? Not from what I hear. The concerns I hear are much more about the lows than the highs.

A practical taper should be more gradual, with 1-3 dB steps being more typical – and which makes it difficult to locate the transitions in the space. If we tapered the bottom 5 boxes at 3-3-3-6-6 dB, we would get an overall LF loss of 1 dB and gain substantial HF steering. The same price would be paid for a taper of 1-1-1-1-2-2-4-4 dB on the bottom 8 boxes of a 16-element array. These are just two of a myriad of options that can be employed to help tailor the response of our bent/broken system to the shape of the audience.

The trade-off for the potential problems this tapering might cause also includes additional benefits: besides increasing front-back level uniformity in the HF range, it also improves uniformity (to a lesser extent) as frequency falls – all the way down. The dB that we lose in the low end is offset by the fact that the beam center is steered upward off the floor and therefore spread more evenly front to back.

Gain Taper Risks Vs Benefits
There are tangible risks to offsetting levels and EQ within a coupled loudspeaker array. Gentle slopes and gradual level transitions will reduce the risk, while steep slopes and transitions will increase it.

There’s potential for phase offset between elements that have different EQ curves, but this should be minimal as long as reasonable EQ is applied.

It’s the impact on dynamic range that merits detailed discussion. Asymmetric EQ and level taper will reduce the dynamic range and potentially cause dynamic shifting, i.e., some parts of the system may reach limiting before others.

This can be a classic TANSTAAFL (There ain’t no such thing as a free lunch) trade-off between maximum uniformity, stability, and headroom. Detectible instability in the frequency and spatial response are unacceptable outcomes. In short, dynamic uniformity is a vital part of level and spatial uniformity.

Level taper affects on dynamic range (Figure 2) can be used as a reference point. This is one area where the program material and usage are extremely relevant. If the system is to be operated at its absolute maximum at all times (e.g., a heavy metal music festival), then front/back level uniformity must yield to maximum dynamic range and stability (level tapering and asymmetric EQ must be absolutely minimized).

By contrast, if the system will be operated with ample headroom under controlled conditions (e.g., musical theater), then asymmetric EQ and level tapering become viable options to maximize uniformity. This decision must be evaluated in the field based on risk and return. 

Figure 2: Log/linear decoder example for combined levels of eight loudspeakers (neglecting phase). Tapering in successive 1 dB increments is shown. The loss from the maximum possible summation is shown in the last column.

My personal approach is generally to compromise, using minimal asymmetric EQ and leveling to reduce, but not necessarily fully eliminate the level increase in the front of the room. Risks are relatively low if the asymmetry can be kept low through a large majority of the array. Increased asymmetry at the bottom has more potential benefit and is less likely to cause audible instability to the majority shareholders above them.

Bear in mind, however, that much of my work is in applications that highly prioritize uniformity and fidelity, which leaves me with more room for asymmetry than those who optimize systems that absolutely must prioritize for maximum stability while delivering bone-crushing power.

Real-world loudspeakers will have variable amounts of overlap over frequency. An array of constant beamwidth models will have an upper range with constant overlap and a lower range with increasing (and variable) overlap. The effectiveness of asymmetric EQ techniques therefore varies over frequency, with the HF range enjoying the lowest side affects and risks.

An array of proportional beamwidth models has proportional overlap, i.e., it rises gradually and steadily with wavelength. Combined EQ can be approached here by segmenting the spectral range into isolated (HF) and overlapped (LF) regions. EQ and level setting for the isolated HF is carried out by the ABC approach (separate EQ for A, B and C as soloists followed by a mutual EQ to compensate for the combined effects).

By contrast, the LF region is approached as a single block, with all EQ and level settings matched (i.e., symmetric). This approach will likely yield less uniformity than the fully asymmetric approach but eliminates the dynamic risks inherent in asymmetric EQ.
We all strive for front/back level uniformity, yet many fear the perils of breaking the line. There’s a limit to how much we can squeeze these systems by splay angle asymmetry alone. The cluster is hung and isn’t coming back down, so we need to look at how much level disparity is still left. If it’s too loud in front, I vote we break the line and turn down the lower boxes, until or unless we know we are reaching the point of dynamic instability. If you have a better measurable and verifiable method, I’d love to hear it.

Theory World
One funny historical aspect related to this subject: 30 years ago when we started utilizing FFT analyzers to tune sound systems, many engineers would deride us. They resisted our use of an analyzer to help make decisions, saying we lived in “theory world” and that they lived in the “real world.”

Nowadays some engineers still want to limit the actions we perform based on the analyzer, but the problem has been flipped on it’s head: we’re the ones living in the real world and they’re living in theory world. Funny that one, eh?

Bob McCarthy has been designing and tuning sound systems for over 30 years. His book Sound Systems: Design and Optimization is available at Focal Press. He lives in NYC and is the director of system optimization for Meyer Sound.